Queremos encontrar maneiras eficientes de descrever e representar objetos em imagens. Idealmente, as representações não deveriam ser alteradas por ruído e transformações geométricas.
Para simplificar os descritores, consideraremos imagens em preto e branco.
Código da cadeia
O código da cadeia é um esquema que foi feito para representar as bordas de um objeto. Dado um ponto inicial pertencente à borda, o código é definido por uma sequência formada pelas direções entre cada pixel e seu vizinho, até que a borda seja fechada.
O espaçamento da grade determina a resolução da codificação. Além disso, vamos considerar que a sequência descreverá um caminho feito no sentido anti-horário.
Para tornar o código da cadeia invariante à translação, podemos adotar um processo de normalização da cadeia. Nós trataremos a sequência da cadeia como um número em base 4 ou base 8 e utilizaremos o código que minimizar este número. Assim, escolhemos sempre o pixel inicial que minimiza o número da sequência.
A invariância de escala pode ser obtida simplesmente variando a escala da grade.
Podemos tornar o código da cadeia invariante quanto à rotação utilizando a primeira diferença do código da cadeia. Suponha que $A = a_0, a_1, \dots, a_{n - 1}$ é o código da cadeia que representa a borda de um objeto. A primeira diferença será dada por $B = b_1, b_1, \dots, b_{n - 1}$ onde $b_k = a_k - a_{k - 1} \pmod n$, sendo $n \in \{4, 8\}$.
Assinatura
Uma assinatura é uma representação unidimensional da borda de um objeto. Uma das formas mais simples é dada pelo gráfico da distância da borda ao centróide em função do ângulo, como ilustrado nas figuras a seguir.
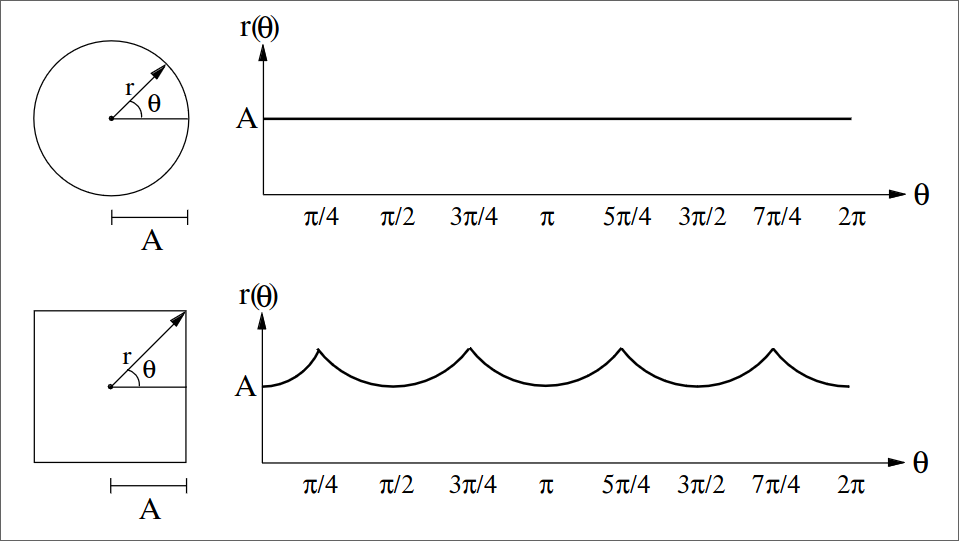
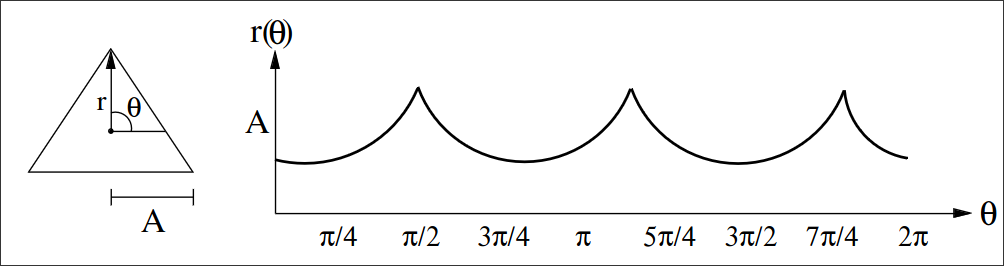
Nesta definição, as assinaturas já são invariantes à translação.
Uma maneira simples de tornar a assinatura invariante à rotação é escolher um ponto de partida comum. Podemos escolher o ponto mais distante do centroide, caso esse seja único.
A invariância com relação à escala pode ser obtida pela normalização dos valores de $r(\theta)$, por exemplo, no intervalo $[0, 1]$.
Fecho convexo
O fecho convexo de uma região planar $R$ corresponde ao menor polígono convexo contendo $R$. Em análise de imagens, o fecho convexo é usado para representar formas poligonais complexas por meio de um polígono mais simples, o qual engloba a forma original. Essa forma mais simples, muitas vezes, é suficiente para permitir o reconhecimento do objeto.
Esqueleto
Vamos reduzir a imagem a uma estrutura mais simples, chamada de esqueleto. Há várias maneiras de construir o esqueleto de um objeto. Algumas delas são:
- Transformada do eixo médio
- Transformada de distância
- Diagrama de Voronoi
- Afinamento de objetos
Diagrama de Voronoi
Seja $S$ um conjunto de $n$ pontos no plano. O diagrama de Voronoi do conjunto $S$ é uma partição do plano em n regiões convexas $V(p)$ ao redor de cada ponto $p$, tal que cada ponto no interior da região $V(p)$ está mais próximo de $p$ do que de qualquer outro ponto em $S$.
Tomando-se as arestas de um diagrama de Voronoi, o resultado é chamado de esqueleto interno do objeto.
Descritores de bordas
Perímetro
O perímetro representa o comprimento da borda de um objeto. Ele é invariante quanto às operações de translação e rotação. Podemos calcular o perímetro de um objeto usando o código da cadeia em vizinhança-8 da seguinte maneira:
$$ P = N_p + \sqrt{2} N_i $$onde $P$ é o perímetro e $N_p$ e $N_i$ representam o número de códigos direcionais pares (componentes horizontal e vertical) e ímpares (componentes diagonais), respectivamente.
Curvatura
A curvatura mede a taxa de variação ao longo do contorno ou da borda do objeto. A curvatura $\kappa$ em um ponto $(x_i, y_i)$ de um contorno planar fechado pode ser determinada por uma mudança na orientação entre os segmentos $\overline{(x_{i - j}, y_{i - j})(x_i, y_i)}$ e $\overline{(x_i, y_i)(x_{i + j}, y_{i + j})}$, ou seja, os segmentos unindo o ponto $(x_i, y_i)$ a dois outros pontos localizados em uma vizinhança $j \geq 1$, conforme mostrado a seguir.
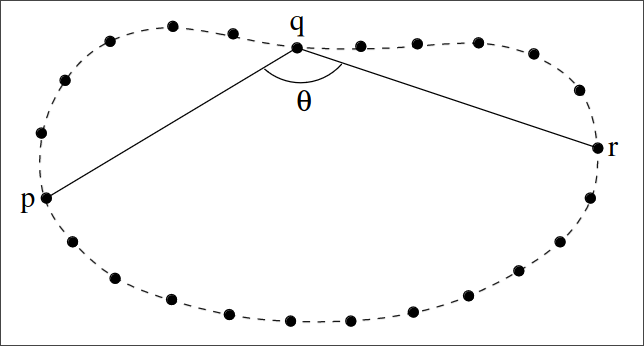
Então, a curvatura é calculada como
$$ \kappa(x_i, y_i) = \arctan{\left(\frac{y_{i + j} - y_i}{x_{i + j} - x_i}\right)} - \arctan{\left(\frac{y_i - y_{i - j}}{x_i - x_{i - j}}\right)} $$Energia de deformação
A energia de deformação pode ser entendida como a energia necessária para ajustar um elástico ou arame à forma desejada da borda. A energia de deformação pode ser calculada como a soma dos quadrados da curvatura $\kappa(\rho)$ da borda sobre o perímetro $L$ da borda, ou seja
$$ E = \frac{1}{L} \sum_{\rho = 1}^L [\kappa(\rho)]^2 $$em que $E \geq \frac{2 \pi}{r}$. O valor mínimo $\frac{2 \pi}{r}$ é obtido para um círculo de raio $r$.
Descritores de região
Nos descritores baseados em região, os pixels localizados no interior da região ou objeto são considerados no cálculo do descritor, em vez de utilizar apenas os pixels que formam a borda da região.
Descritores de região incluem:
- Área
- Compacidade ou Circularidade
- Projeções horizontal e vertical
- Número de Euler
- Momentos
- Eixos maior e menor
- Excentricidade
- Retângulo envolvente
- Convexidade
- Retangularidade
- Solidez
- Descritores sintáticos ou relacionais