Le modèle sténopé

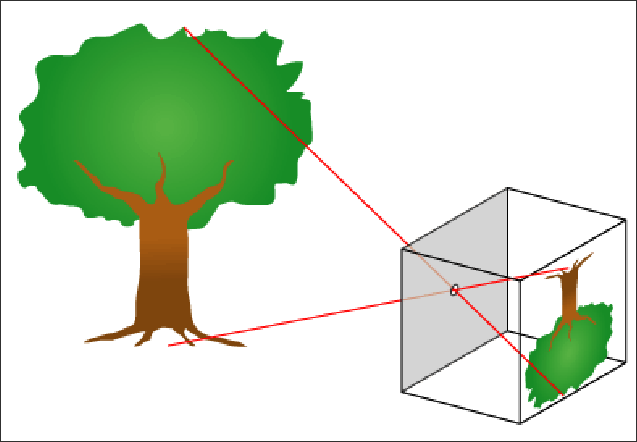
La première manière trés simple d’acquérir des images, c’est avec le modèle sténopé. Ici, une partie de la lumière issue de l’objet passe par une petite trou d’ouverture $O$ et se projette sur le plan focal. Nous faisons comme ça pour que chaque point de l’objet soit représenté par un rayon. Sinon, l’image ne serait pas formée.

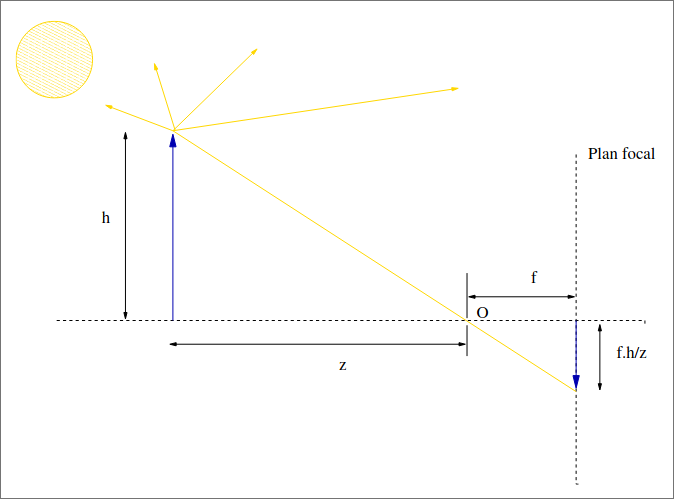
La distance $f$ est appelée distance focale. Supposons qu’on a le modèle suivant pour décrire le sténopé:

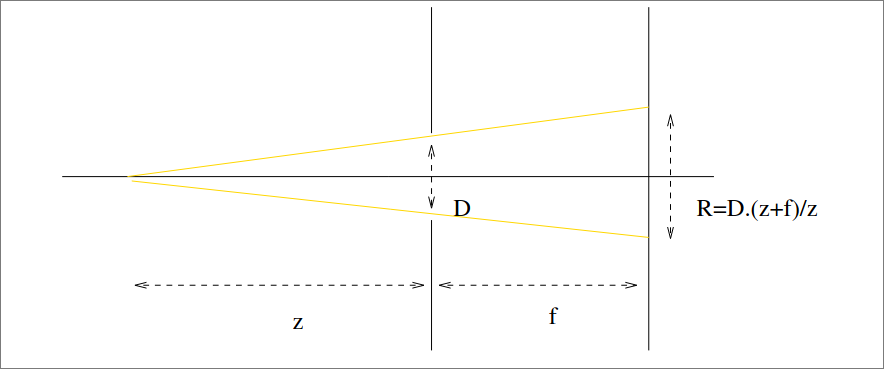
Puisque l’ouverture $O$ est finie, les rayons produisent du flou. Cet effet peut être modélisé par

$$ g_z \ast S $$

où $S$ serait l’image “réel” et $g_z$ est la fonction indicatrice d’un disque de rayon $\frac{(z + f) D}{z}$.

Note
Une fonction indicatrice sur un ensemble $E$ est nulle n'importe où sauf dans $E$, où elle est toujours $1$.

L’utilisation de lentilles

Pour avoir une image plus nette, nous pouvons ajouter une lentille. Elle se comporte comme indiqué dans l’image suivante.

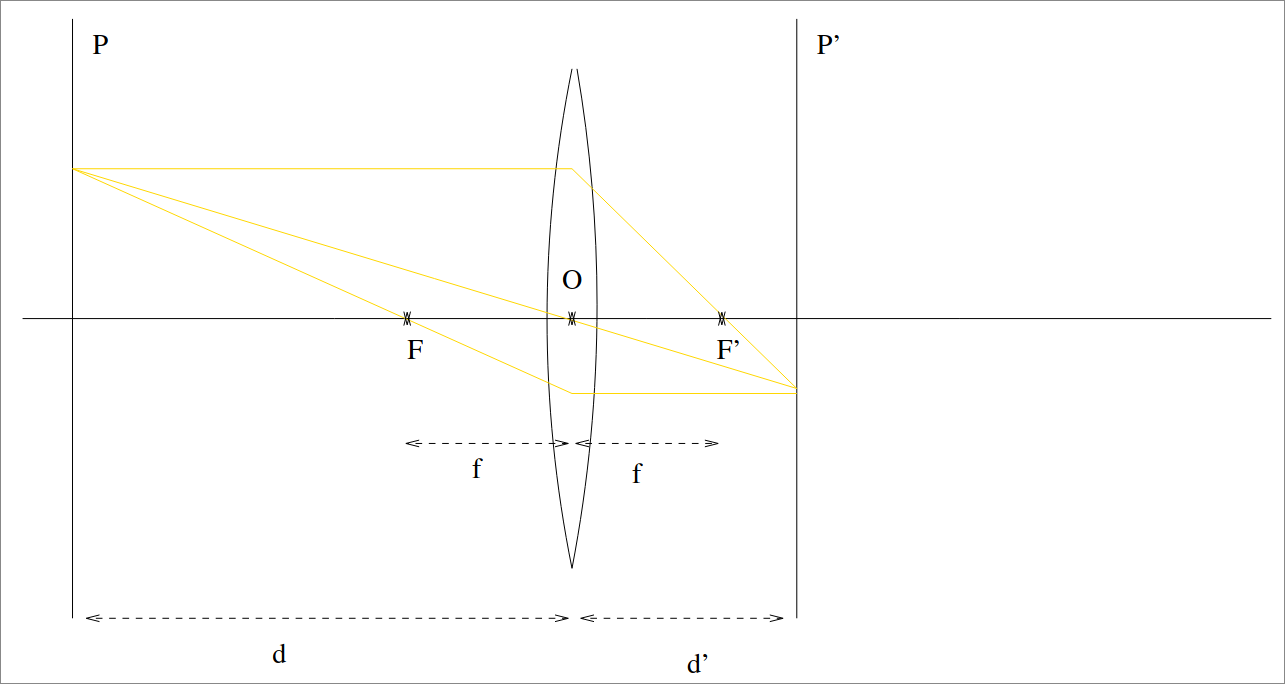
À retenir:

  1. Les rayons qui passent à l’horizontal convergent au point focal;
  2. Les rayons qui passent par l’origine $O$ ne changent pas;
  3. Les rayons qui passent par une point focal sortent à l’horizontal.

Il est possible de calculer la distance focale $f$ avec la Relation de Descartes.

$$ \frac{1}{d} + \frac{1}{d^\prime} = \frac{1}{f} $$

Profondeur de champ

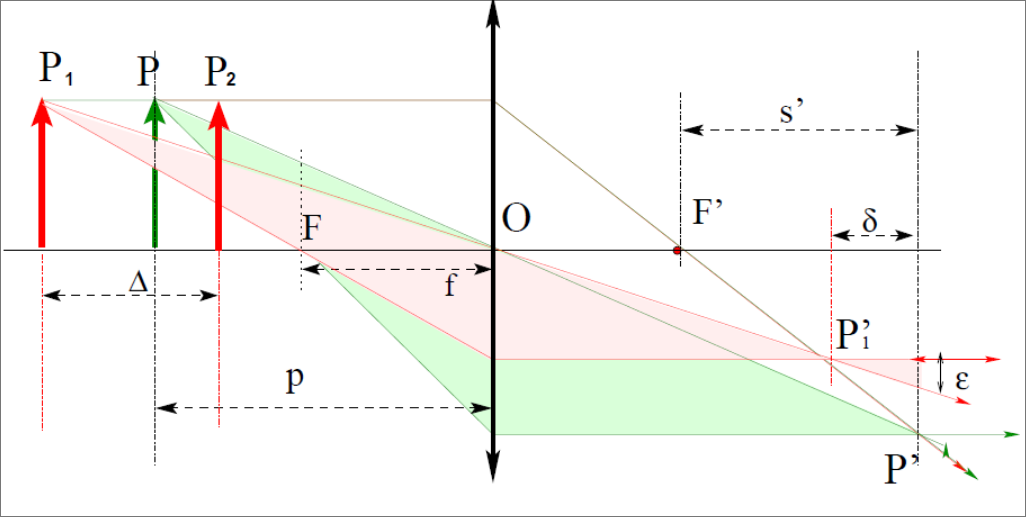
La profondeur de champ est la distance séparant l’objet net le plus proche de l’appareil de l’objet net le plus lointain.

$$ \Delta \approx \frac{2 \varepsilon p^2}{D f} $$

où $p$ est la distance de l’objet.

Info
Le nombre d'ouverture $N$ est défini par $N = \frac{f}{D}$. D'habitude, il apparait en progression géométrique (à $q = \sqrt{2}$) et est représenté par $f / \cdot$.
  • e.g. $f / 4$ signifie $N = 4$.

Quand $N$ augmente (à $f$ constant):

  1. $\Delta$ augmente;
  2. Les défauts de diffraction augmentent;
  3. Les défauts de vignettage (image plus sombre près du bord) augmentent;

Echantillonnage

Maintenant, le but, c’est de transformer les photons de l’image en quelque chose électrique qui peut être digitalisé.

$$ \left( f \colon \mathbb{R}^2 \mapsto \mathbb{R} \right) \rightarrow (\{f(k)\}_{k \in \Omega}). $$

On peut formaliser mathématiquement la comptage des photons par une convolution avec $g_{\text{capt}}$, qui est la fonction indicatrice du capteur.

$$ I_{i, j} = (I \ast g_{\text{capt}})(i, j) $$

L’image suivante présente une example de grille de capteurs.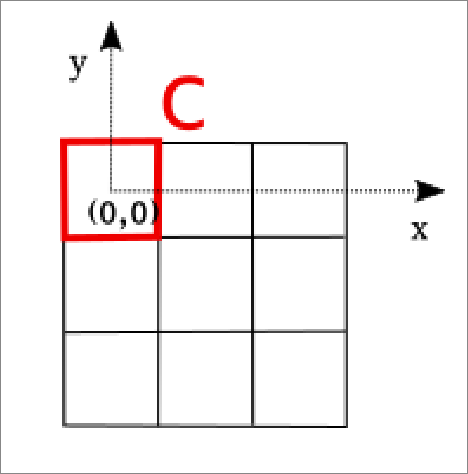

L’échantillonnage d’une fonction $f$ en un point $\mathbf{x}$ est modélisé par

$$ f \cdot \delta_{\mathbf{x}} $$

Donc, pour modéliser l’acquisition des images, nous allons utiliser le peigne de Dirac, $\Pi_\Gamma$, qui est défini prochainement.

$$ \Pi_\Gamma = \sum_{\gamma \in \Gamma} \delta_\gamma $$

où $\Gamma$ est l’ensemble de positions où les détecteurs sont placées (e.g. $\Gamma \subset \mathbb{N}^2$).

Nous pouvons aussi places les détecteurs en un réseau hexagonal. Ça peut apporté des avantages parfois.

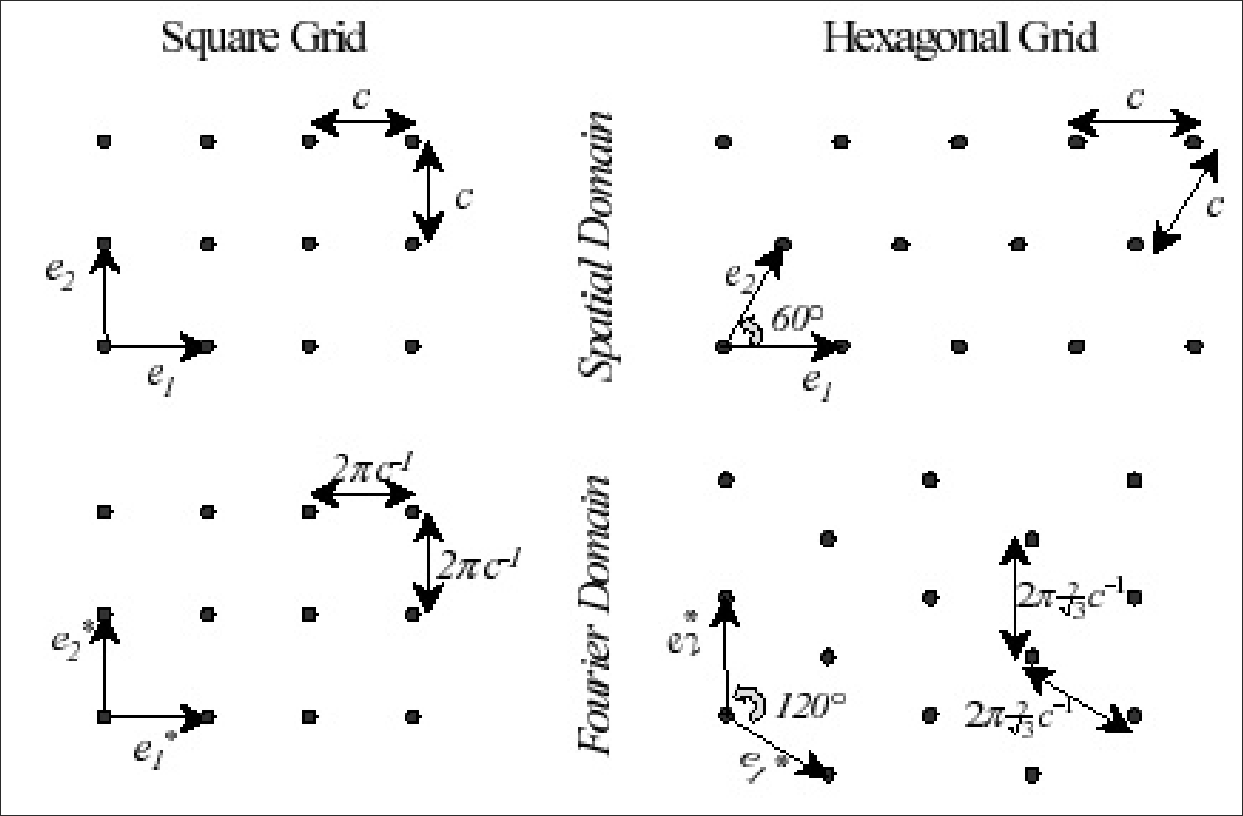
Modèle d’acquisition

Le modèle complet d’acquisition peut être résumé par l’équation suivante:

$$ u = Q[h((g \ast s) \Pi_\Gamma F + b)] $$

où:

  • $s$ est la scène, c’est-à-dire l’image continue et “réelle”;
  • $g$ est la réponse impulsionnelle du système optique et de l’intégration des capteurs $(g_\text{ouv} \ast g_\text{flou} \ast g_\text{fil} \ast g_\text{capt})$;
    • $g_\text{ouv}$ est l’ouverture;
    • $g_\text{flou}$ est le flou;
    • $g_\text{fil}$ est le filtre;
    • $g_\text{capt}$ est le capteur;
  • $\Pi_\Gamma$ est le peigne de Dirac;
  • $F = \mathbb{1}_\Omega$, $\Omega \subset \mathbb{R}^2$, support de l’acquisition;
  • $b$ est un bruit additif;
  • $h$ est une fonction croissant qui mesure le changement de contrate;
  • $Q$ est un opérateur de quantification;
  • $u$ est l’image acquise;

Modèle de bruit

Nous allons noter $v$ l’image discrète après échantillonnage et $u$ l’image bruitée. Il y a 3 principaux types de bruit:

  1. Bruit additif: $u(i, j) = v(i, j) + b(i, j)$ où les $b(i, j)$ sont i.i.d.;
  2. Bruit impulsionnel: $u(i, j) = v(i, j) A(i, j) + (1 - A(i, j))B(i, j) où $A(i, j)$ sont des variables de Bernoulli i.i.d. et $B(i, j)$ des variables i.i.d. (e.g. sel et poivre);
  3. Bruit multiplicatif: $u(i, j) = v(i, j) b(i, j)$ où les $b(i, j)$ sont i.i.d.

Le modèle de bruit peut être simplifié et résumé par la distribution suivante:

$$ I_\text{bruit} = \mathcal{N}(g C \tau + \mu_R, g^2 C \tau + \sigma_R^2) $$

où

  • $g$ est le gain (ISO);
  • $\tau$ est le temps d’acquisition;
  • $C$ est la radiance (photons / temps);
  • $\mu_R$ et $\sigma_R^2$ sont les moyenne et variance du bruit de lecture.

Transformée de Fourier

Pour $f \in L^1(\mathbb{R}^2)$,

$$ \mathcal{F}(f)(\omega) = \hat{f}(\omega) = \int_{\mathbb{R}^2} f(\mathbf{x}) e^{- i \mathbf{x} \omega} \; \text{d} \mathbf{x} $$
Note
$\hat{f}$ est continue et tende à 0 à l'infini.
$$ \mathcal{F^{-1}}(\hat{f})(\mathbf{x}) = f(\mathbf{x}) = \frac{1}{(2 \pi)^2} \int_{\mathbb{R}^2} \hat{f}(\omega) e^{i \mathbf{x} \omega} \; \text{d} \omega $$

Quelques propriétés importantes:

  1. $\mathcal{F}(f \ast g) = \mathcal{F}(f) \cdot \mathcal{F}(g)$;
  2. $\mathcal{F}(f \cdot g) = \frac{1}{(2 \pi)^2} \mathcal{F}(f) \ast \mathcal{F}(g)$;
  3. $\mathcal{F}(f(\mathbf{x} - \mathbf{a})) = e^{- i \omega \mathbf{a}} \mathcal{F}(f(\mathbf{x}))$;
  4. $\mathcal{F}(e^{i \mathbf{a} \mathbf{x}} f(\mathbf{x}))(\omega) = \mathcal{F}(f(\mathbf{x}))(\omega - \mathbf{a})$;

Néanmoins, puisque les images sont des objets discrets, nous allons utiliser la transformée de Fourier discrète. Généralement, la transformée de Fourier est montrée par un graphe du logarithme du module de chaque fréquence. Les points au centre du spectre sont des fréquences basses.

Des intuitions relevantes du spectre de Fourier:

  1. Les basse fréquences contient la plus grande part de l’information de l’image. Ça, c’est la raison pour laquelle le centre est plus blanc;
  2. Les lignes à un angle $\theta$ à l’image sont des rayons blanches à un angle $\theta + 90^\circ$ au spectre de Fourier.
  3. Par des propriétés des transformées de Fourier, lorsque il y a une translation à l’image, il n’y a que une difference de phase au spectre de Fourier (le module reste le même); De plus, s’il y a une rotation, le spectre se fait translater (la phase reste la même).
  4. Les convolutions à l’image original peut être effectuées par une simple multiplication du spectre de Fourier (fonction indicatrice d’un disque centrée à l’origine est un filtre passe-bas).

Le repliement

Si la fréquence d’échantillonnage est plus petit que le limite de Nyquist, le signal sera sous-échantillonné. Ainsi, nous aurons une perte d’informations.

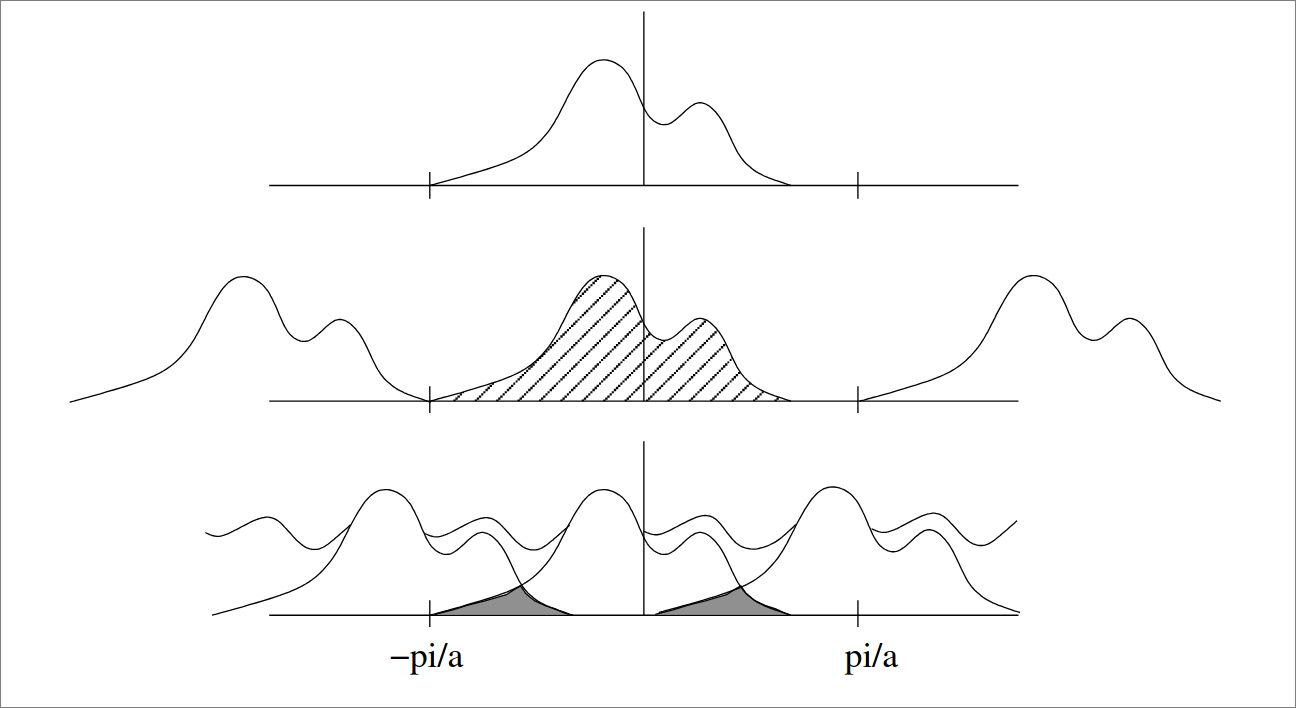
Si une image a un repliement, on peut réduire les défauts avec un filtre passe-bas, mais le spectre est fondamentalement détérioré de manière irréversible. Le repliement apparait généralement comme une “pixellisation” de l’image.

Le ringing

Le phénomène de ringing apparait lorsque une image sous-échantiollionné est soumise à un filtre passe-bas qui est une fonction indicatrice carrée dans le domaine de Fourier.

$$ \mathcal{F}^{-1}[\mathcal{F}(f \times \mathbb{1}_K)] = \mathcal{F}^{-1}[\mathcal{F}(f)] \ast \mathcal{F}^{-1}(\mathbb{1}_K) = f(x, y) \ast \mathrm{sinc}(x, y) $$

L’application d’un filtre passe-bas est donc equivalent à une convolution de l’image par une fonction sinc. Ainsi, l’image résultant montre le ringing: une genre d’ondulation près des bordures d’une image.

Exercises