In mathematical morphology, the basic structure of an image is a complete lattice.
A complete lattice is a set $K$ equipped with an order relation $\leq$ that satisfies:
- Reflexivity: $\forall x \in K$, $x \leq x$;
- Antisymmetry: $\forall x, y \in K$, $x \leq y$ and $y \leq x$ implies $x = y$;
- Transitivity: $\forall x, y, z \in K$, $x \leq y$ and $y \leq z$ implies $x \leq z$;
- $\forall x, y \in K$, the supremum and infimum of $x$ and $y$ exist and are denoted $x \lor y$ and $x \land y$ respectively.
We will focus on the boolean lattice and the function lattice.
Binary images
We will consider 0 begin black and 1, white.
From now on, we will consider 1-dimensional images and represent them in the following way:
$$ X = \{k \colon x_k = \mathrm{True}\} $$this means that our image is a set of indices, representing where the image is 1 (white).
In this sense,
$$ \begin{align*} X \lor Y &= X \cup Y \\ X \land Y &= X \cap Y \end{align*} $$Consider the following two images:

Compute $X \lor Y$.
Then,
$$ \begin{align*} X &= \{1, 2, 3\} \\ Y &= \{2, 3, 4, 5\} \end{align*} $$So, $X \lor Y = X \cup Y = \{1, 2, 3, 4, 5\}$.
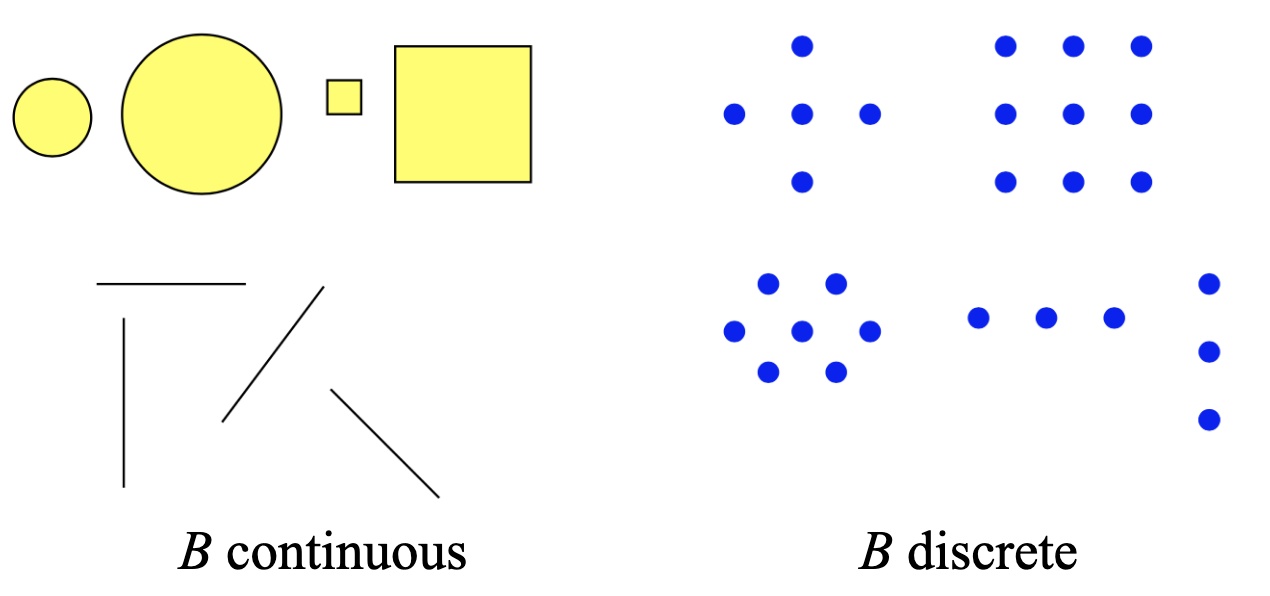
Structuring element
The structuring element, which we will denote as $B$ in the following, is defined by its:
- Shape;
- Size;
- Origin (not necessarily in $B$).
Dilation and erosion
The dilation and erosion are order-preserving operations. The dilation uses the Minkowski addition and the erosion, the Minkowski subtraction.
Let $X$ be an image and $B$, a structuring element. Then,
$$ \begin{align*} \mathcal{D}(X, B) &= X \oplus B = \{ x + b \mid x \in X, b \in B \} \\ \mathcal{E}(X, B) &= X \ominus B = \{ z \mid \forall b \in B, z + b \in X \} \\ \end{align*} $$There are some important properties of the dilation and erosion.
Dilation:
- Commutativity: $X \oplus B = B \oplus X$;
- Associativity: $(X \oplus Y) \oplus B = X \oplus (Y \oplus B)$;
- $X \subseteq Y \implies X \oplus B \subseteq Y \oplus Y$;
- $(X \cup Y) \oplus B = (X \oplus B) \cup (Y \oplus B)$;
- Extensivity: $O \in B \implies X \subseteq X \oplus B$.
Erosion:
- $(X \ominus Y) \ominus B = X \ominus (Y \oplus B) = (X \ominus B) \ominus Y$
- $X \ominus B = (X^c \oplus B)^c$
- $X \subseteq Y \implies X \ominus B \subseteq Y \ominus Y$;
- $(X \cap Y) \ominus B = (X \ominus B) \cap (Y \ominus B)$;
- Anti-extensivity: $O \in B \implies X \ominus B \subseteq X$.
An easy way to compute $X \oplus B$ is to place the origin of $B$ on top of each pixel in $X$. If there is an intersection between $B$ and $X$ at this point, then it is 1.
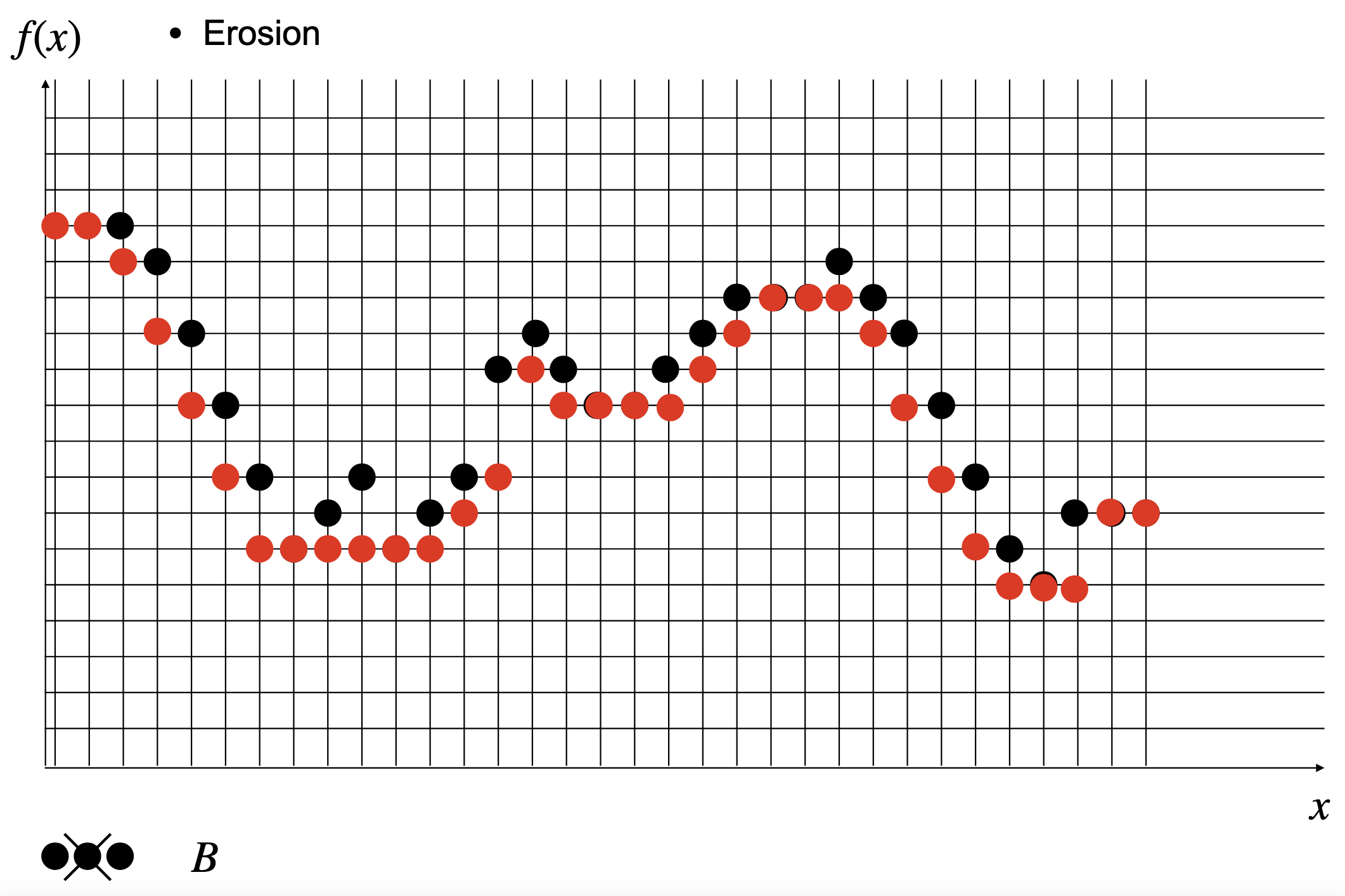
For $X \ominus B$, we can do the same. However, we assign 1 to a pixel only if $B$ is completely contained in $X$.
Opening and closing
$$ \begin{align*} X \circ B = X_B = \mathcal{D}(\mathcal{E}(X, B), B) \\ X \bullet B = X^B = \mathcal{E}(\mathcal{D}(X, B), B) \end{align*} $$Some interesting properties of the opening and closing:
- $X \subseteq Y \implies X_B \subseteq Y_B$;
- $X \subseteq Y \implies X^B \subseteq Y^B$;
- Idempotency: $(X_B)_B = X_B$ and $(X^B)^B = X^B$;
- Extensivity: $X \subseteq X^B$;
- Anti-extensivity: $X_B \subseteq X$;
- Duality: $X^B = ((X^c)_B)^c$.
Grayscale images
To work with grayscale images, we will use functions instead of sets to represent the images. Our first step is to redefine the operations of supremum and infimum we have been using.
Let $\mathcal{F} = \{f_1, \dots, f_n\}$ be a set of functions. Then,
$$ \begin{align*} (\sup \mathcal{F})(x) &= \sup \{ f_1(x), \dots, f_n(x) \} \\ (\inf \mathcal{F})(x) &= \inf \{ f_1(x), \dots, f_n(x) \} \\ \end{align*} $$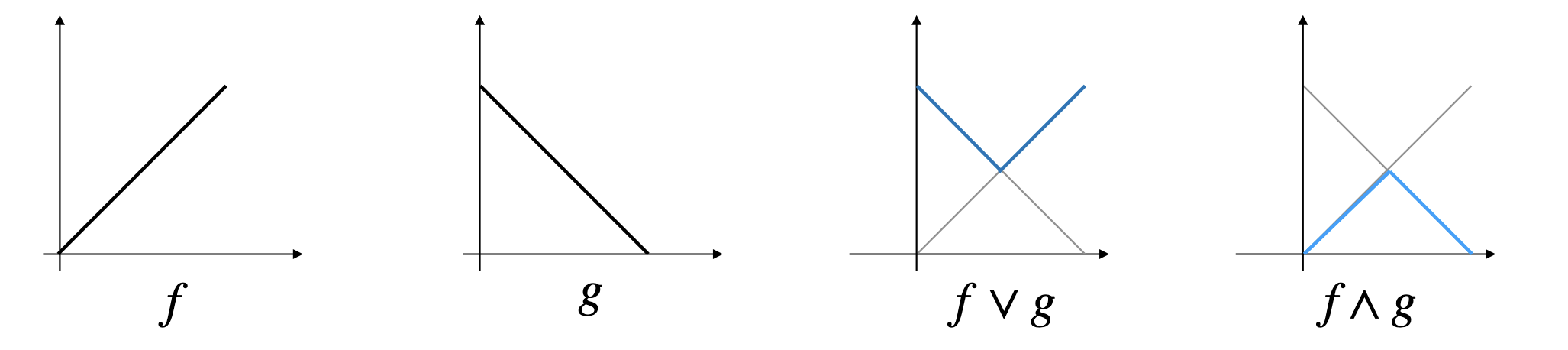
Also, the structuring element is now a function instead of a set.
Let $f$ be a grayscale image and $B$, a structuring function. Then,
$$ \begin{align*} [\mathcal{D}(f, B)](x) &= \sup \{ f(y) \mid y \in \check{B}_x \} \\ [\mathcal{E}(f, B)](x) &= \inf \{ f(y) \mid y \in B_x \} \\ \end{align*} $$Warning: in dilation, we use the reflection of $B$, $\check{B}$.
Some properties of the dilation and erosion:
- $f \leq g \implies \mathcal{D}(f, B) \leq \mathcal{D}(g, B)$;
- $f \leq g \implies \mathcal{E}(f, B) \leq \mathcal{E}(g, B)$;
- $\mathcal{D}(f \lor g, B) = \mathcal{D}(f, B) \lor \mathcal{D}(g, B)$;
- $\mathcal{E}(f \land g, B) = \mathcal{E}(f, B) \land \mathcal{E}(g, B)$;
The opening and closing are the same as in the binary case.
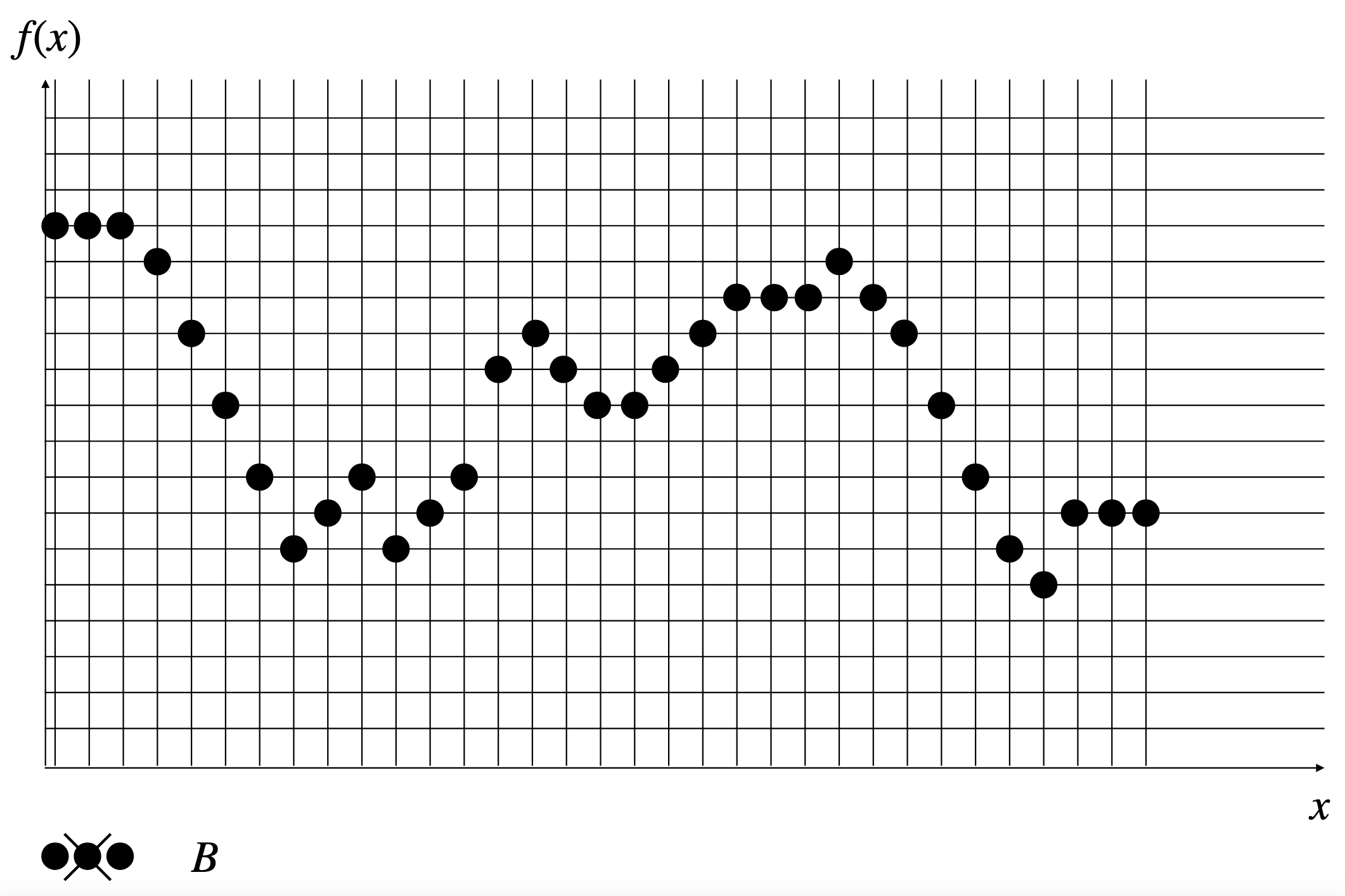
Original image:
Erosion:
Opening:

Applications
Gradient of image
We can compute the gradient of an image using the dilation and erosion operations:
$$ | \nabla f | = \mathcal{D}(f, B) - \mathcal{E}(f, B) $$Top-hat
The top-hat transformation extracts small elements and details.
$$ T(f) = f - f \circ B = f - f_B $$