Interpolation, geometric transformations and filtering

Interpolation

Our goal is to calculate the value of a pixel that is outside the grid of the image. To this end, we will interpolate the image.

Depending on our hypothesis, we can arrive to different interpolation methods.

1. Constant by parts: nearest neighbor;
2. Continue: bi-linear;
3. Polynomial of degree 3: bi-cubic;
4. Limited band: Shannon interpolation.

Method	Initialization	Operations per pixel
Nearest neighbor	$0$	$1$
Bi-linear	$0$	$4$
Bi-cubic	$4 N ^2$	$16$
Shannon	$0$	$N^2$

We will call our discrete image $I_d$ and the continuous image after interpolation $I_c$.

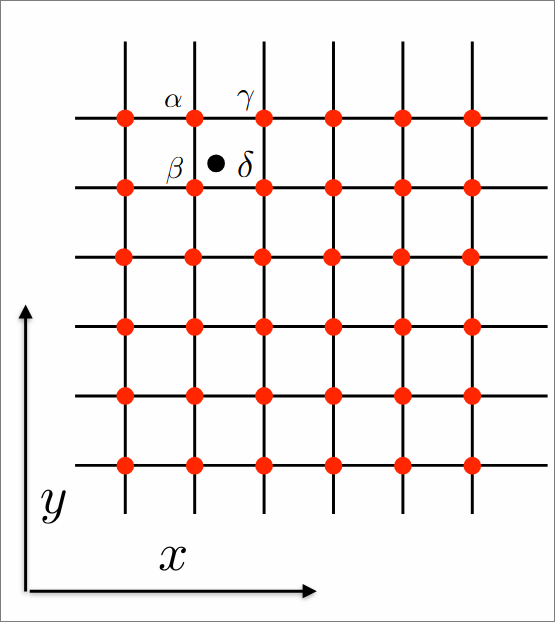
In the following example grid, where $\alpha, \beta, \gamma, \delta$ are the corner pixel values and we try to estimate the pixel in the black dot (we will call $\xi$).

Nearest neighbor

$$ I_c(x, y) = I_d(\lfloor x + 0.5 \rfloor, \lfloor y + 0.5 \rfloor) $$

This function can also be expressed as a convolution:

$$ I_c = I_d \ast T_0, \qquad T_0(x, y) = \begin{cases} 1 & \vert x \vert, \vert y \vert < 0.5 \\ 0 & \text{otherwise} \end{cases} $$

Bi-linear interpolation

Now, we suppose that $I_d$ is piecewise linear. To simplify our notation, we will consider $i_0 = \lfloor x \rfloor$, $j_0 = \lfloor y \rfloor$, $x_F = x - i_0$ and $y_F = y - j_0$. Then,

$$ \begin{align*} I_c(x, y) = & x_F \times y_F \times I_d(i_0 + 1, j_0 + 1) \\ & + (1 - x_F) \times y_F \times I_d(i_0, j_0 + 1) \\ & + x_F \times (1 - y_F) \times I_d(i_0 + 1, j_0) \\ & + (1 - x_F) \times (1 - y_F) \times I_d(i_0, j_0) \end{align*} $$

We can also express this interpolation as a convolution:

$$ I_c = I_d \ast T_1, \qquad T_1(x, y) = \begin{cases} (1 - \vert x \vert) (1 - \vert y \vert) & \vert x \vert, \vert y \vert < 1 \\ 0 & \text{otherwise} \end{cases} $$

Here, $T_1$ is a triangular function.

Bi-cubic interpolation

For the cubic case, we suppose that $I_c$ and its two first derivatives are continuous. Then, we consider the following function:

$$ h(x) = \begin{cases} \frac{\vert x \vert^3}{2} - x^2 + \frac{2}{3} & \vert x \vert \leq 1 \\ -\frac{\vert x \vert^3}{6} + x^2 - 2 \vert x \vert + \frac{4}{3} & 1 \leq \vert x \vert \leq 2 \\ 0 & \vert x \vert > 2 \end{cases} $$

With the function $h$, we can interpolate $I_d$ as:

$$ I_c(x, y) = \sum_n \sum_k c_{k, n} h(y - n) h(x - k) $$

The coefficients $c_{k, n}$ need to be calculated. Since the support of $h$ has a size of 4, it suffices to find 16 coefficients to interpolate each pixel $(x, y)$. The only good reason to find all coefficients is if the whole image will be interpolated. Otherwise, it is useless.

Shannon interpolation

If an image was well sampled, the Shannon theorem assures us the following interpolation:

$$ I_c(x, y) = \sum_{k, n} I_d(k, n) \mathrm{sinc}(x - k) \mathrm{sinc}(y - n) $$

Clearly, this is not the most efficient method, since it uses all points to compute a single interpolation. However, this interpolation can be efficiently computed if $(x, y) = (m \times 2^{-d}, l \times 2^{-d})$, where $m, l \in \mathbb{Z}$.

Geometric transformations

Here, we consider how to apply geometric transformations to images. These transformations might be translations, rotations, scaling, etc. All of these transformations can be expressed by matrices.

Scaling by $S_x \times S_y$	Rotation by $\theta$	Translation by $(\delta_x, \delta_y)$
$\begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} = \begin{pmatrix} S_x & 0 \\ 0 & S_y \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$	$\begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$	$\begin{pmatrix} x^\prime \\ y^\prime \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & \delta_x \\ 0 & 1 & \delta_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$

We can, therefore, express any geometric transformation by a matrix $T$. The way we apply the transformation is by, first, creating a new image $J$. Then, for each pixel $(i, j)$ in $J$ we compute the following:

$$ J(i, j) = I_c(T^{-1}(i, j)) $$

and, then, we can fill up the new image $J$. Note that the interpolation is necessary to do this operation.

Filtering

Filtering is an operation that transforms the image into another with the same dimensions. Every filtering operation can be expressed as a convolution.

$$ J = I \ast K $$

where $K$ is the convolution kernel that describes which filter is being applied.

Linear filtering

We say that a filter is linear if its operator is linear and the filtering is invariant on translation. A simple example of a linear filter is the average:

$$ K = \begin{pmatrix} \frac{1}{k^2} & \dots & \frac{1}{k^2} \\ \vdots & \ddots & \vdots \\ \frac{1}{k^2} & \dots & \frac{1}{k^2} \end{pmatrix} $$

A more advanced example is computing the gradient of an image:

$$ \begin{align*} \partial_x &= I \ast \begin{pmatrix} 1 & -1 \end{pmatrix} \\ \partial_y &= I \ast \begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{align*} $$

Denoising filters

There are many filters that can be used to denoise images.

1. Median filter: instead of calculating the average, it selected the median of a region.
2. Bilateral filter: we take an weighted average of the pixels values. The weights are determined by how close each pixel is to the center, both in regards to distance and gray level. It has two parameters: $\sigma_s$ (the window size) and $\sigma_I$ (how close the grey levels need to be).
3. Non-local averages filter: similar do the bilateral filter, but tries to keep textures in the image (that would otherwise be erased).