Perception

Color is the result of 3 things:

  1. An illuminant: source of light ($I(\lambda)$);
  2. An object: absorbs and reflects light ($R(\lambda)$);
  3. An observer: sensor ($S(\lambda) = I(\lambda) R(\lambda)$).

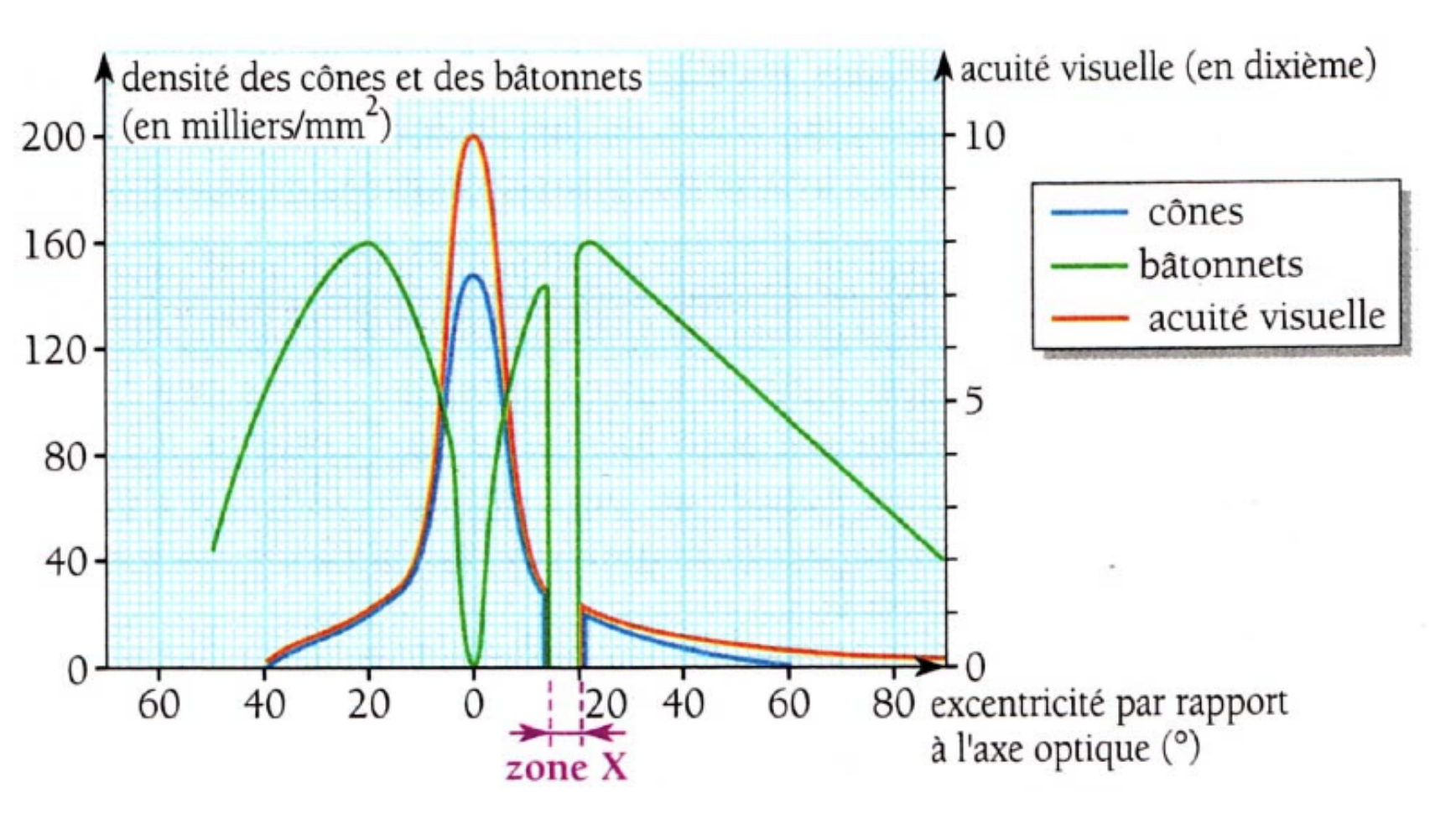
Our visual system consists of rods (sensible, imprecise) and cones (not so sensible, very precise). There are three types of cones:

  • S (short) cones: blue;
  • M (medium) cones: green;
  • L (large) cones: red;

Let $s(\lambda)$, $m(\lambda)$ and $l(\lambda)$ be the spectral sensibilities of these cones. Then, we perceive a spectrum $S(\lambda) = I(\lambda) R(\lambda)$ as three values:

$$ \begin{align*} P_1 &= \langle S, s \rangle = \int_{\lambda_\text{min}}^{\lambda_\text{max}} s(\lambda) S(\lambda) \; \mathrm{d} \lambda \\ P_2 &= \langle S, m \rangle = \int_{\lambda_\text{min}}^{\lambda_\text{max}} m(\lambda) S(\lambda) \; \mathrm{d} \lambda \\ P_3 &= \langle S, l \rangle = \int_{\lambda_\text{min}}^{\lambda_\text{max}} l(\lambda) S(\lambda) \; \mathrm{d} \lambda \end{align*} $$
Note
The triplet $(P_1, P_2, P_3)$ that we perceive can never be equal to $\mathbf{e}_i$, where $i \in \{1, 2, 3\}$.

The following figure shows all possible combinations of $(P_1, P_2, P_3)$ in $\mathbb{R}^3$.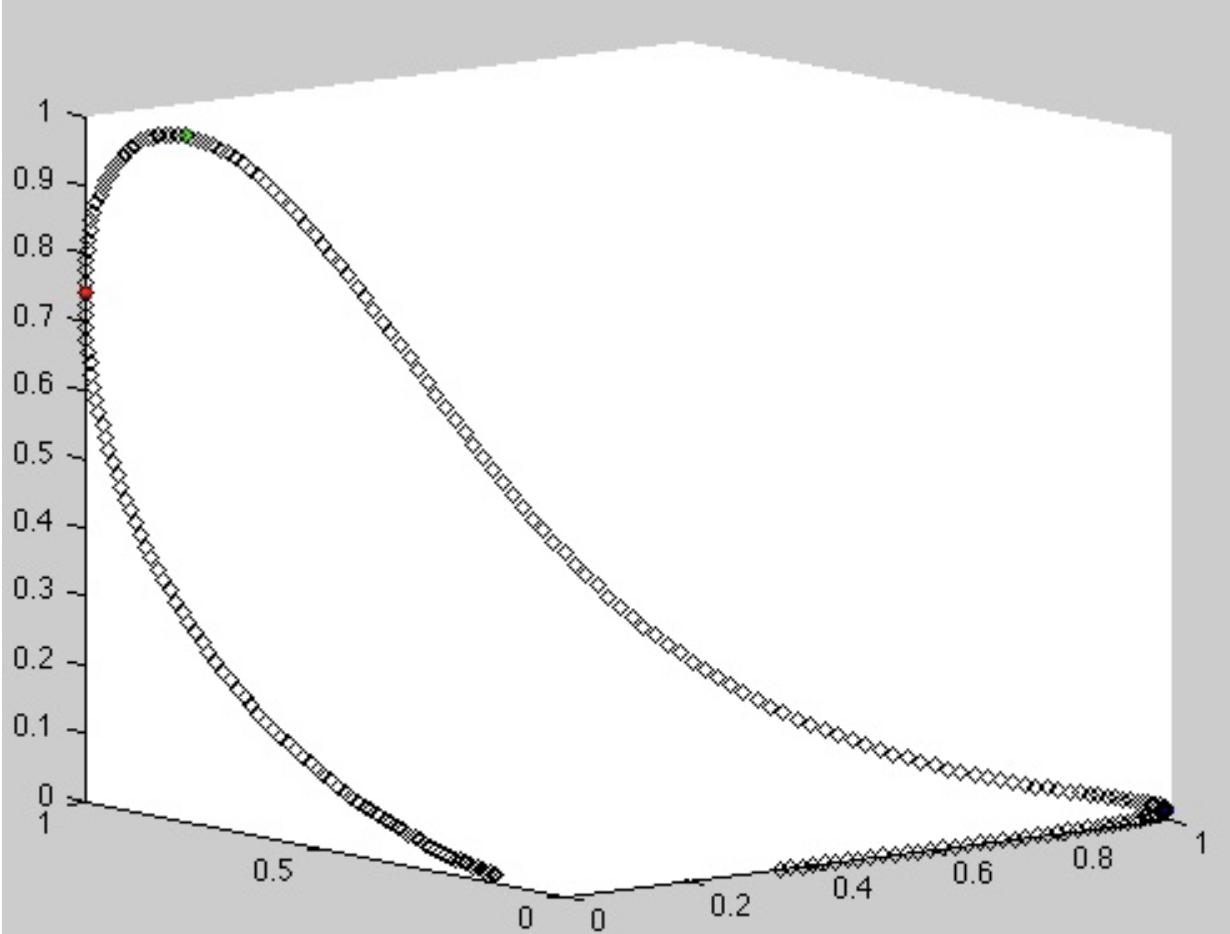

An interesting consequence of the way we perceive colors is that, depending on $I(\lambda)$, two objects $R_1(\lambda)$ and $R_2(\lambda)$ may be seen as having the same color (even if they do not).

White balance

The idea is to do a linear transformation in each color channel. If the illuminant has a color $(R_0, G_0, B_0)$, then we apply the following transformation:

$$ T \colon (R, G, B) \to \left( \frac{R_1}{R_0} R, \frac{G_1}{G_0} G, \frac{B_1}{B_0} B \right) $$

where $(R_1, G_1, B_1)$ represents the reference illuminant. There are many ways to estimate $(R_0, G_0, B_0)$:

  • Gray world: global average of channels
  • White patch: usage of the brightest pixels.

Color spaces

In order to better represent colors digitally, we restrict the colors perceived to those which $P_1 + P_2 + P_3 = 1$. This gives rise to a bi-dimensional space.

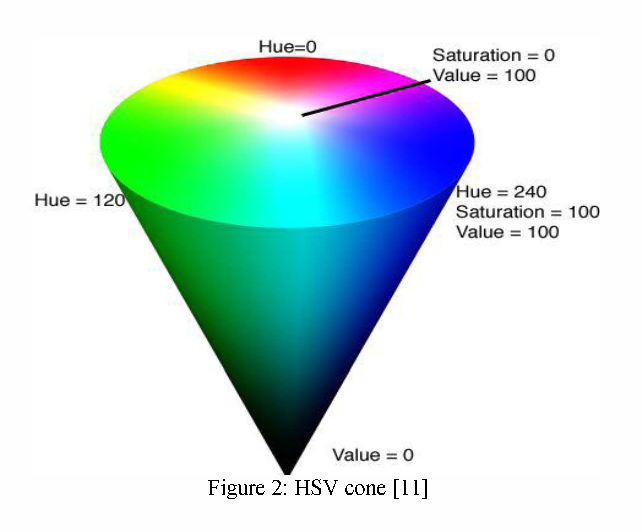
Alternative representative spaces (HSV)

With HSV, we separate the Hue (color), Saturation and Lightness. With such a model, we are able to apply all 1-dimensional algorithms to colored images using the lightness.

Color capturing

When a RAW photo is taken, a Bayer filter is usually used to capture the colors.

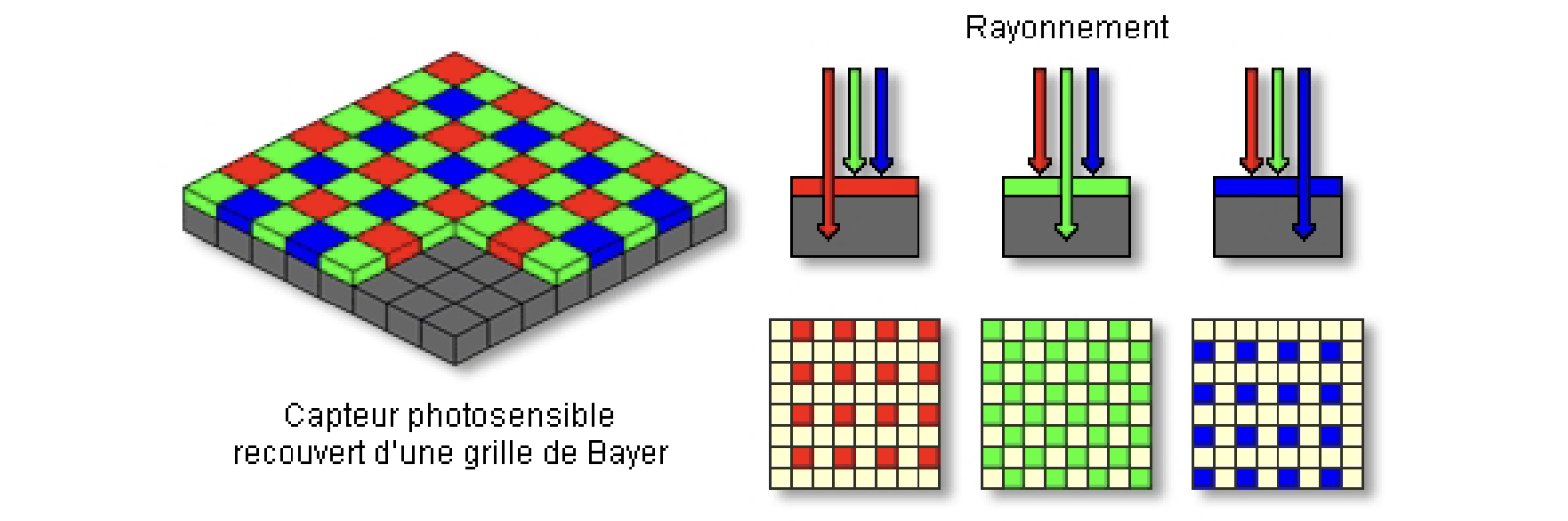
Each of the colors in the grid has 12 bits. Our job is to transform the 12 bits of each color pixel into a multi-colored pixel of 24 bits (8 bits per channel). This process is known as demosaicing (détramage). To this end, we interpolate the RAW image to find the color of each pixel.

Nowadays, it is also common to use neural networks to demosaice the RAW image.