We present different methods to test data against hypotheses.
Statistical test
We consider the null hypothesis ($H_0$) and the alternative hypothesis ($H_1$). We are interested in rejecting or not the null hypothesis.
Here, let $\delta$ denote the decision function used to reject or not the null hypothesis.
$$ \delta(x) = \begin{cases} 0 & \text{do not reject $H_0$} \\ 1 & \text{reject $H_0$ in favor of $H_1$} \end{cases} $$Parametric model
In parametric models, the hypotheses form a subset of the parameters:
$$ \begin{align*} H_0 &\rightarrow \Theta_0 \\ H_1 &\rightarrow \Theta_1 \\ \end{align*} $$where $\Theta_0 \cap \Theta_1 = \emptyset$.
Our goal is to control the Type-I error rate:
$$ \alpha = \sup_{\theta \in \Theta_0} \mathbb{P}_\theta(\delta(X) = 1) $$The quality of the test is then computed through $\beta$:
$$ \forall \theta \in \Theta_1 \quad \beta(\theta) = \mathbb{P}_\theta(\delta(X) = 0) $$A statistical test $\delta$ is uniformly most powerful (UMP) at level $\alpha$ if for any other test $\delta^\prime$ such that
$$ \alpha = \sup_{\theta \in \Theta_0} \mathbb{P}(\delta(X) = 1) \geq \sup_{\theta \in \Theta_0} \mathbb{P}(\delta^\prime(X) = 1), $$we have
$$ \forall \theta \in \Theta_1 \quad \beta(\theta) = \mathbb{P}(\delta(X) = 0) \leq \mathbb{P}(\delta^\prime(X) = 0). $$The existence of an UMP test is not guaranteed. From now on, we assume $\Theta \subseteq \mathbb{R}$ and that the model is dominated, i.e., it has a density function $p_\theta(x)$.
Simple hypotheses
For these kinds of hypothesis, it is always possible to find an UMP test at level $\alpha$. Let $p_0 = p_{\theta_0}$ and $p_1 = p_{\theta_1}$ the probability measures under hypotheses $H_0$ and $H_1$.
The following test is UMP for any $c > 0$.
$$ \delta(x) = \mathbb{1}_{\frac{p_1(x)}{p_0(x)} > c} $$Consider the Gaussian model $\mathcal{P} = \{P_\theta \sim \mathcal{N}(\theta, 1) \mid \theta \in \mathbb{R} \}$. The hypotheses are $H_0 = \{\theta_0 = 0\}$ and $H_1 = \{\theta_1 = 2\}$ and there is a single observation. Then, the likelihood ratio is:
$$ \frac{p_1(x)}{p_0(x)} = \frac{e^{-\frac{(x - 2)^2}{2}}}{e^{-\frac{x^2}{2}}} \propto e^{2x} $$Since this is an increasing function of $x$, any test of the form $\mathbb{1}_{x > c}$ is UMP.
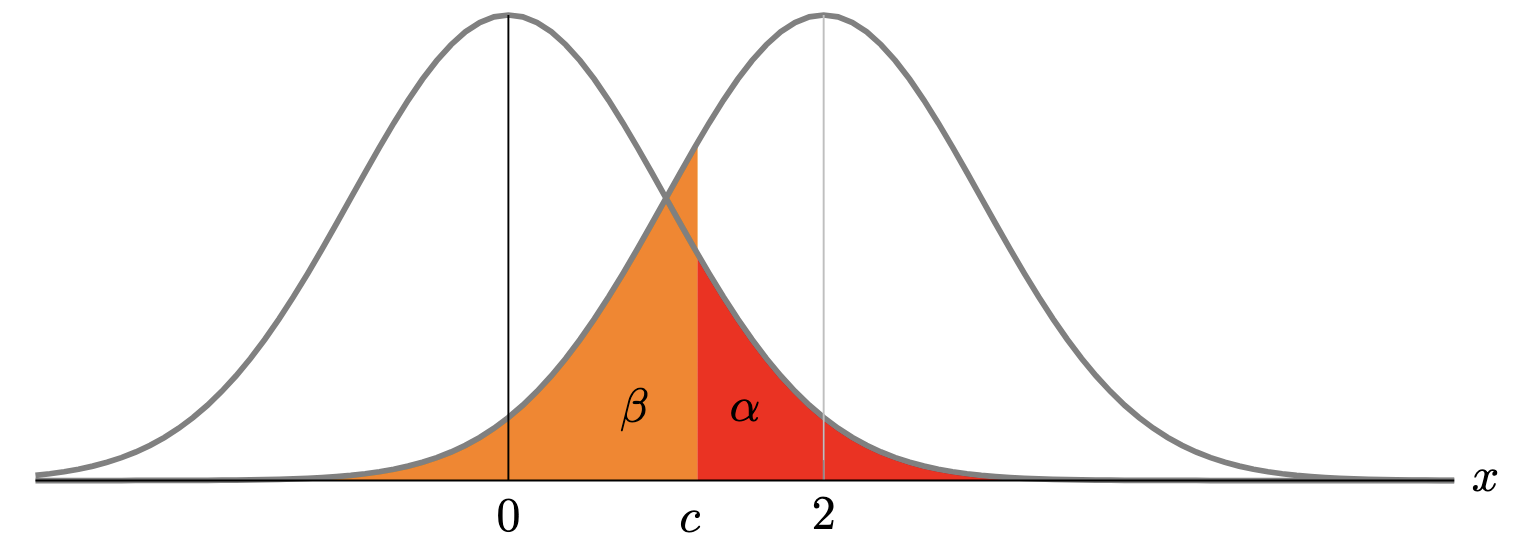
We can also calculate $\alpha$ and $\beta$ for this test. Let $Z \sim \mathcal{N}(0, 1)$. Then,
$$ \begin{align*} \alpha &= \mathbb{P}_0(\delta(x) = 1) = \mathbb{P}_0(X > c) = \mathbb{P}(Z > c) \\ \beta &= \mathbb{P}_1(\delta(x) = 0) = \mathbb{P}_1(X \leq c) = \mathbb{P}(Z \leq c - 2) \end{align*} $$One-tailed test
For one-tailed tests, it is possible to find an UMP test if the likelihood ratio is monotone:
$$ \forall \theta^\prime > \theta, \quad \frac{p_{\theta^\prime}(x)}{p_{\theta}(x)} = f(T(x)), $$where $T$ is a statistic and $f$ is an increasing function.
If the likelihood ratio is monotone, the following test is UMP for any $c > 0$.
$$ \delta(x) = \mathbb{1}_{T(x) > c} $$Consider the Gaussian model $\mathcal{P} = \{P_\theta \sim \mathcal{N}(\theta, 1) \mid \theta \in \mathbb{R} \}$. The hypotheses are $H_0 = \{\theta \leq 0\}$ and $H_1 = \{\theta > 0\}$. Then, the likelihood ratio is:
$$ \forall \theta^\prime > \theta, \quad \frac{p_{\theta^\prime}(x)}{p_\theta(x)} = \frac{e^{-\frac{(x - \theta^\prime)^2}{2}}}{e^{-\frac{(x - \theta)^2}{2}}} \propto e^{(\theta^\prime - \theta) x} $$Since this is an increasing function of $x$, any test of the form $\mathbb{1}_{x > c}$ is UMP.
We can also calculate $\alpha$ and $\beta$ for this test. Let $Z \sim \mathcal{N}(0, 1)$. Then,
$$ \begin{align*} \alpha &= \sup_{\theta \leq 0} \mathbb{P}_\theta(\delta(X) = 1) \\ &= \sup_{\theta \leq 0} \mathbb{P}_\theta(X > c) \\ &= \sup_{\theta \leq 0} \mathbb{P}(Z > c - \theta) \\ &= \mathbb{P}(Z > c) \\ \forall \theta > 0, \quad \beta(\theta) &= \mathbb{P}_\theta(\delta(X) = 0) = \mathbb{P}_\theta(X \leq c) = \mathbb{P}(Z \leq c - \theta) \end{align*} $$If the function $f$ is decreasing, then the test takes the following format.
$$ \delta(x) = \mathbb{1}_{T(x) < c} $$Two-tailed test
Let us first consider an example. Consider the Gaussian model $\mathcal{P} = \{P_\theta \sim \mathcal{N}(\theta, 1) \mid \theta \in \mathbb{R} \}$. The hypotheses are $H_0 = \{\theta = 0\}$ and $H_1 = \{\theta \neq 0\}$. We are also considering the following test:
$$ \delta(x) = \mathbb{1}_{|x| > c} $$The Type-I error of $\delta$ is:
$$ \alpha = \mathbb{P}_0(|X| > c) = 2 \mathbb{P}(Z > c) $$with $Z \sim \mathcal{N}(0, 1)$. The Type-II error rate is:
$$ \forall \theta \neq 0, \quad \beta(\theta) = \mathbb{P}_\theta(|X| \leq c) = \mathbb{P}(Z \in [\theta - c, \theta + c]). $$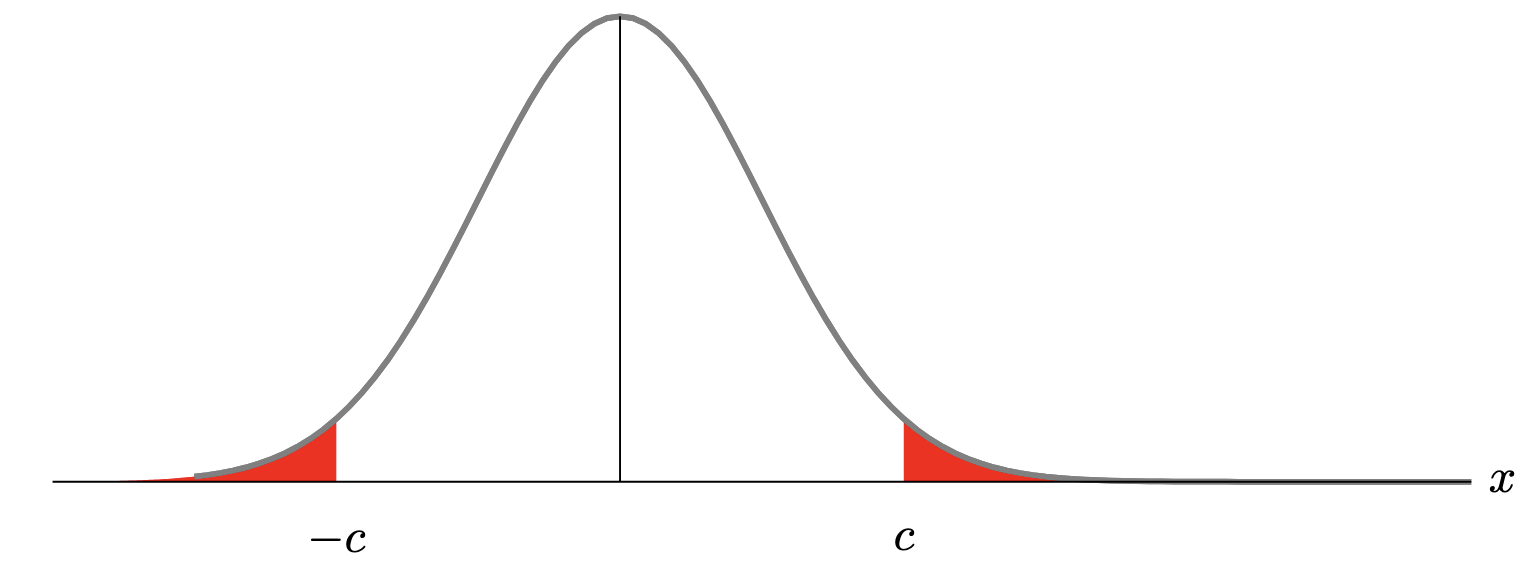
Now, consider the test:
$$ \delta^\prime(x) = \mathbb{1}_{x > c^\prime} $$Assume that $c^\prime$ is chosen in such a way that $\delta^\prime$ also has level $\alpha$:
$$ \alpha = 2 \mathbb{P}(Z > c) = \mathbb{P}_0(X > c^\prime) = \mathbb{P}(Z > c^\prime) $$It must follow that $c^\prime < c$.
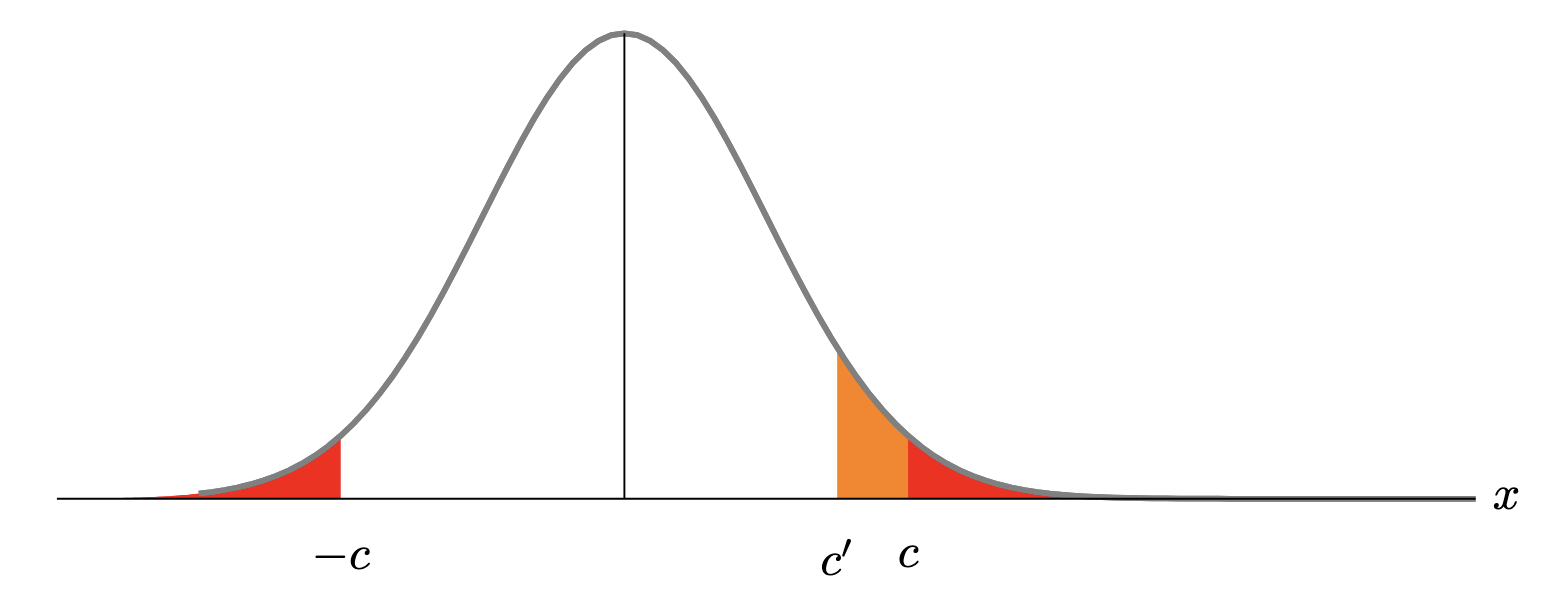
Then, it follows that for sufficiently large $\theta$, $\delta^\prime$ is more powerful than $\delta$:
$$ 1 - \beta^\prime(\theta) = 1 - \mathbb{P}_\theta(X \leq c^\prime) = \mathbb{P}_\theta(X > c^\prime) > \mathbb{P}_\theta(|X| > c) = 1 - \mathbb{P}_0(|X| \leq c) = 1 - \beta(\theta) $$This example shows that there is no UMP test for the two-tailed test.
A test is unbiased if the probability of rejecting $H_0$ against $H_1$ is always higher under $H_1$:
$$ \forall \theta_0 \in \Theta_0, \forall \theta_1 \in \Theta_1, \quad \mathbb{P}_{\theta_1}(\delta(X) = 1) \geq \mathbb{P}_{\theta_0}(\delta(X) = 1). $$Equivalently, a test is unbiased if the probability of accepting $H_0$ is always higher under $H_0$:
$$ \forall \theta_0 \in \Theta_0, \forall \theta_1 \in \Theta_1, \quad \mathbb{P}_{\theta_0}(\delta(X) = 0) \geq \mathbb{P}_{\theta_1}(\delta(X) = 0). $$Observe that, in the previous example, $\delta^\prime$ is biased since
$$ \forall \theta < 0, \quad \mathbb{P}_\theta(\delta^\prime(X) = 1) = \mathbb{P}_\theta(X > c^\prime) < \mathbb{P}_0(X > c^\prime) = \mathbb{P}_0(\delta^\prime(X) = 1). $$On the other hand, the test $\delta$ is unbiased:
$$ \forall \theta \neq 0, \quad \mathbb{P}_\theta(\delta(X) = 1) = \mathbb{P}_\theta(|X| > c) \geq \mathbb{P}_0(|X| \geq c) = \mathbb{P}_0(\delta(X) = 1). $$Thus, we are interested in uniformly most powerful tests among all unbiased tests (UMPU test).
Consider a parametric model in the exponential family:
$$ p_\theta(x) = h(x) e^{\eta(\theta) T(x) - A(x)} $$with $T(x) \in \mathbb{R}$ and $\eta$ an increasing function. Then, there exist an UMPU test of the following form:
$$ \delta(x) = \mathbb{1}_{T(x) \not \in [c_1, c_2]}. $$Consider the Gaussian model with hypotheses $H_0 = \{\theta = 0\}$ and $H_1 = \{\theta \neq 0\}$. We have:
$$ p_\theta(x) \propto e^{-\frac{1}{2} (x - \theta)^2} \propto e^{-\frac{x^2}{2}} e^{x \theta} $$The corresponding function $\eta(\theta) = \theta$ is increasing, so there exists an UMPU test of the form:
$$ \delta(x) = \mathbb{1}_{x \not \in [c_1, c_2]}. $$By symmetry, this test has the form $\delta(x) = \mathbb{1}_{|x| > c}$ as considered previously.