Tip: Vectorial product rule

Let $F, G \colon \mathbb{R}^n \to \mathbb{R}^n$. Then,

$$ \nabla (F(X)^\top G(X)) = \nabla F(X)^\top G(X) + \nabla G(X)^\top F(X) $$
$$ \DeclareMathOperator*{\argmax}{arg \,max \,} \DeclareMathOperator*{\argmin}{arg \,min \,} $$

Without constraints

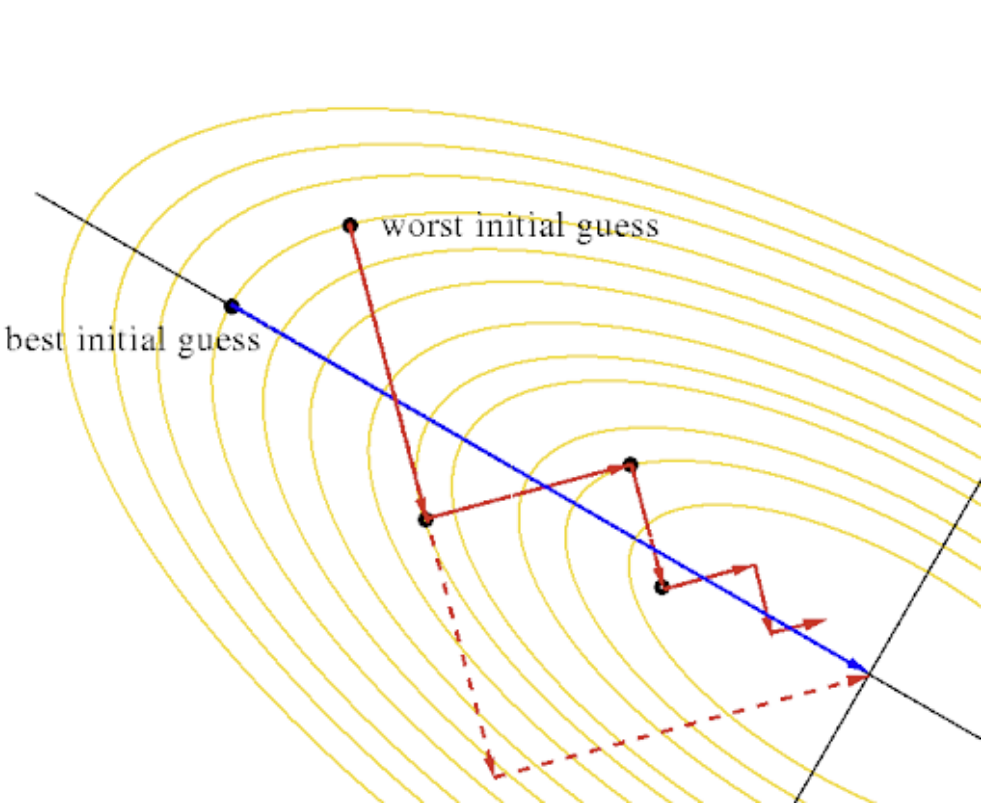
We are interested in minimizing an arbitrary function $f \colon \mathbb{R}^n \to \mathbb{R}$. To do so, we will use the gradient descent method. Let $\mathbf{x}^{(0)} \in \mathbb{R}^n$ be a random starting point. Then, for $k \in \mathbb{N}$,

$$ \mathbf{x}^{(k + 1)} = \mathbf{x}^{(k)} - s^{(k)} \nabla f(\mathbf{x}^{(k)}). $$

where $s^{(k)}$ is the step size.

We can find the step size that minimizes the function $f$:

$$ s^{(k)} = \argmin_{s \geq 0 } f(\mathbf{x}^{(k)} - s \nabla f(\mathbf{x}^{(k)})) $$

This $s^{(k)}$ is such that

$$ \begin{align*} \frac{\mathrm{d}}{\mathrm{d} s} [f(\mathbf{x}^{(k)} + s \nabla f(\mathbf{x}^{(k)}))] &= 0 \\ \implies [\nabla f(\mathbf{x}^{(k)} + s^{(k)} \nabla f(\mathbf{x}^{(k)}))]^\top [- \nabla f(\mathbf{x}^{(k)})] &= 0 \\ \implies [\nabla f(\mathbf{x}^{(k+1)})]^\top [\nabla f(\mathbf{x}^{(k)})] &= 0 \end{align*} $$

In other words, the direction of the step is always perpendicular to the direction of the previous step.

Newton’s method

We can also use a quadratic approximation of the gradient. Let $H(\mathbf{x}) = \nabla^2 f(\mathbf{x})$ be the Hessian matrix of $f$.

$$ [H(\mathbf{x})]_{ij} = \frac{\partial^2 f(\mathbf{x})}{\partial x_i \partial x_j} $$

Then, we can minimize $f$ by following the sequence defined below:

$$ \mathbf{x}^{(k + 1)} = \mathbf{x}^{(k)} - [H(\mathbf{x}^{(k)})]^{-1} \nabla f(\mathbf{x}^{(k)}). $$

Put simply, our step size is the inverse of the Hessian matrix.

With constraints

We consider now $m$ inequality constraints and $p$ equality constraints:

$$ \begin{cases} g_i(\mathbf{x}) \leq 0, & i \in I = \{1, \dots, m\} \\ h_j(\mathbf{x}) = 0, & j \in j = \{1, \dots, p\} \\ \end{cases} $$

Then, our feasible region is

$$ X = \{\mathbf{x} \in \mathbb{R}^n \mid g_i(\mathbf{x}) \leq 0, \; h_j(\mathbf{x}) = 0, \; \forall i \in I, \; \forall j \in J \} $$

Our problem is therefore to find

$$ \mathbf{x}^\ast = \min_{\mathbf{x} \in X} f(\mathbf{x}) $$
Definition: Coercive function

We say $f \colon \mathbb{R}^n \to \mathbb{R}$ is a coercive function if it tends to infinity in any direction.

$$ \lim_{\Vert \mathbf{x} \Vert \to \infty} f(\mathbf{x}) = \infty $$
Theorem

If $X$ is non-empty and $f$ is coercive, then

$$ \exists \mathbf{x}^\ast = \min_{\mathbf{x} \in X} f(\mathbf{x}) $$