Page Rank
Let $G = (V, E)$ be a web graph. Each node $v \in V$ represents a web page, while there is a directed edge from $u \in V$ to $v \in V$ if $u$ has a hyperlink to $v$. The importance of $v$ is proportional to the importance of nodes linking to $v$.
Let $\delta_\text{in}(v)$ and $\delta_\text{out}(v)$ be the in and out degrees of $v$ in $G$. Then we can define the matrix $M$ as follows:
$$ M_{ij} = \begin{cases} \frac{1}{\delta_\text{out}(v_j)} & \text{if $(v_j, v_i) \in E$} \\ 0 & \text{if $(v_j, v_i) \not \in E$} \end{cases} $$we can also write $M$ as $M = A^\top \times \Delta_\text{out}^{-1}$ where $A$ is the adjacency matrix of $G$ and $\Delta_\text{out}$ is a diagonal matrix whose entries are $\delta_\text{out}(v)$. In other words, one can obtain $M$ by transposing the adjacency matrix and dividing each column by the number of $1$s in the column.
Let $\pi = (\pi_1, \dots, \pi_n)$ be a vector where $\pi_i$ represents the importance of node $v_i$. We want to find $\pi$ such that $M \pi = \pi$ and $\sum_{i=1}^n \pi_i = 1$. The first constraint guarantees that the importance of each node depends on the importance of the nodes that link to it. The second constraint ensures that the importance of each page is normalized.
Consider the following graph:
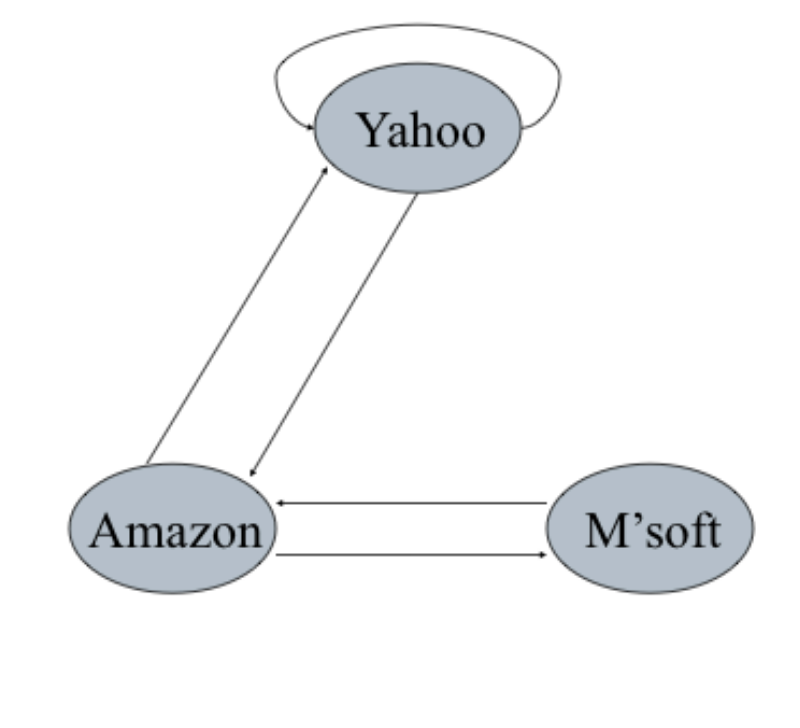
Let us find $M$.
$$ \begin{align*} A = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} &\implies A^\top = \begin{pmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \\ &\implies M = \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 1 \\ 0 & \frac{1}{2} & 0 \end{pmatrix} \end{align*} $$Problems:
- Solution to $M \pi = \pi$ might not be unique;
- Very expensive! Requires $\Omega(n^3)$.
Random surfer
We will model the problem using Markov chains. Consider a random surfer that starts to surf the web at step $0$. Suppose that at step $t$, he is in page $v_i$. Then, the probability that he goes to $v_j$ in the next step is $M_{ji}$.
So, from now on, our definition of importance will be the probability of the random surfer to go to a specific page. Let $\pi_j^{(t)}$ be the probability of visiting page $v_j$ in step $t$. We want to compute $\pi^{(t + 1)}$. Indeed, we have:
$$ \pi^{(t + 1)} = M \pi^{(t)} $$This strategy has some problems, though:
- Which value of $t$ should we choose?
- $\pi^{(t)}$ might depend on the starting node;
- Can we compute this efficiently?
- Spider-traps and Dead-ends.
A spider-trap is a set $S$ of web pages that are not linked to the rest of the graph (i.e. to $V \setminus S$).
A dead-end is a web page that has no links to other pages. We are going to assume dead-ends do not exist.
To solve these problems, we will use jumps:
- At each step, the surfer follows a link with probability $\beta$;
- He can also jump to a random page with probability $(1 - \beta)$.
Then, we define a new stochastic matrix $A_{ij} = \beta M_{ij} + \frac{1 - \beta}{n}$. As before, the probability of going from $v_i$ to $v_j$ is $A_{ji}$. Usually, $\beta \in [0.8, 0.9]$.
Due to performance issues, we compute $\pi^{(t + 1)}$ as following:
$$ \pi^{(t + 1)} = A \pi^{(t)} = \beta M \pi^{(t)} + \left[ \frac{1 - \beta}{n} \right]_n $$Input: A directed graph $G$, $0 < \beta < 1$ and $\epsilon > 0$.
Output: Page Rank vector $\pi$.
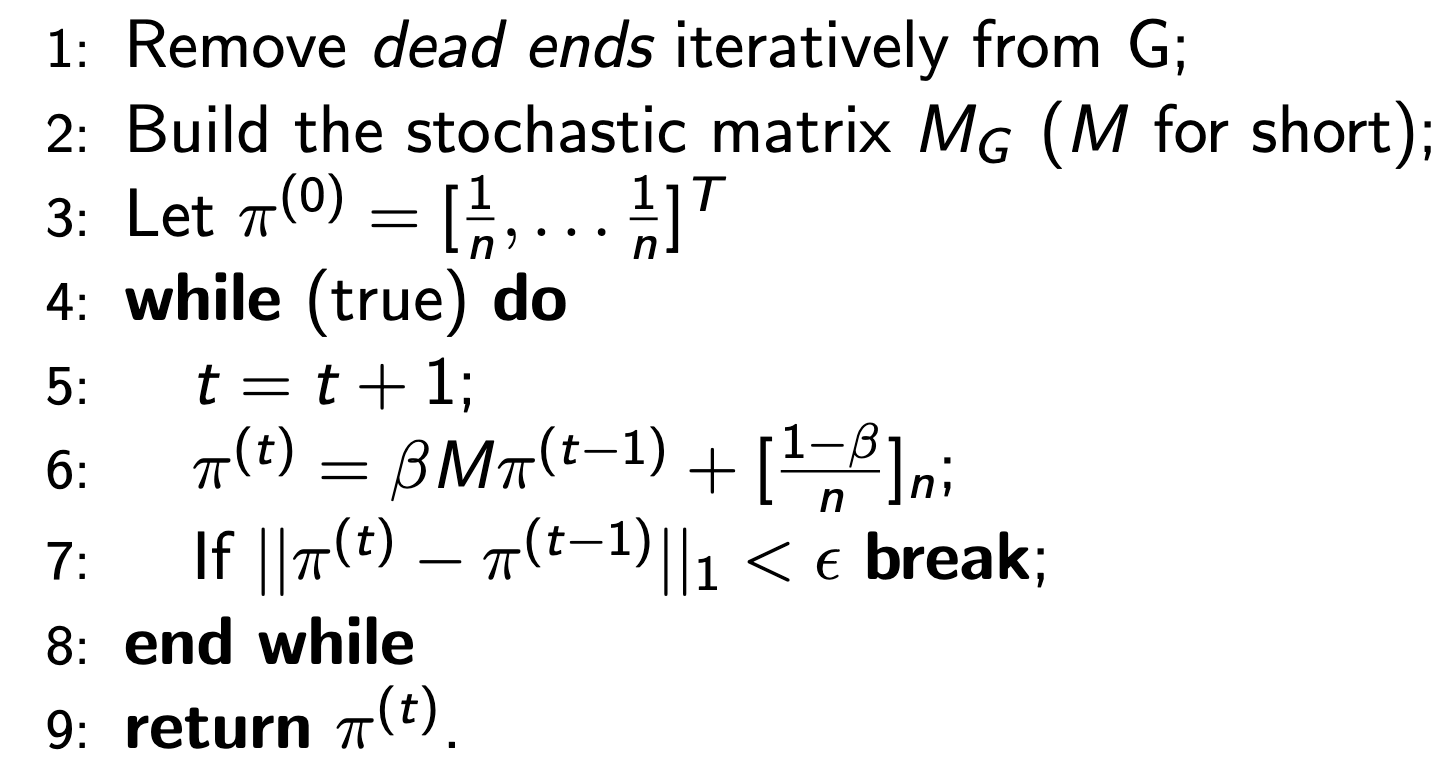
It can be shown that this algorithm converges to a unique solution.
A probability distribution $\pi$ over the states of the Markov chain is called a stationary distribution if
$$ \pi = M \pi $$A Markov chain is called irreducible iff for any $i, j$ there is $n > 1$ such that
$$ M_{ij}^n > 0 $$In other words, there is a finite path between any two states.
A state $i$ has period $k$ if any return to $i$ occurs at step $k \times \ell$, for some $\ell > 0$. Formally,
$$ k = \gcd \{ n \mid \mathbb{P}(X_n = i \mid X_0 = i) > 0 \}. $$If $k = 1$, then the state is said to be aperiodic. A Markov chain is called aperiodic if every state is aperiodic.
With random jumps, the Markov chain of the random surfer is irreducible and aperiodic. Thus, the algorithm converges to the stationary distribution of the Markov chain, $\pi$.
Community detection
Problem: Given a graph $G$, a set $S$ of seed nodes, an integer $k > 0$, find $k$ additional nodes belonging to the “same community” of $S$.
To solve this problem, we will use a variation of the Page Rank algorithm (Page Rank with Restart). We will consider the following matrix $R$:
$$ R_{ij} = \begin{cases} \frac{1}{|S|} & \text{if $v_i \in S$} \\ 0 & \text{otherwise} \end{cases} $$Then, the Page Rank matrix $A$ will be $A_{ij} = \beta M_{ij} + (1 - \beta) R_{ij}$.
With this PR algorithm,
$$ \text{Recall} = \frac{|P \cap C|}{|C \setminus S|} $$where $P$ is the set of nodes found by the algorithm and $C$ is the set of nodes in the community (unknown to us at first).
Advantages:
- It is simple to compute;
- Converges rapidly (2-3 iterations).
Disadvantages:
- We do not know which $k$ to choose;
- Other values of $\beta$ might be good.